גיבוש המודל | ניסוי וטעייה | פתור את המודל
השתמש בפותר ב לְהִצטַיֵן למצוא את זרימה מקסימלית מצומת S לצומת T ברשת מכוונת. נקודות ברשת נקראות צמתים (S, A, B, C, D, E ו- T). קווים ברשת נקראים קשתות (SA, SB, SC, AC וכו ').
גיבוש המודל
המודל שאנו הולכים לפתור נראה כדלקמן ב- Excel.

1. לנסח זאת בעיית זרימה מקסימלית , ענה על שלוש השאלות הבאות.
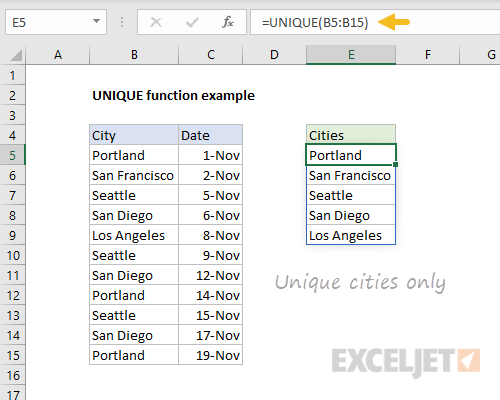
א. מה ההחלטות שצריך לקבל? לבעיה זו, אנו זקוקים לאקסל כדי למצוא את הזרימה על כל קשת. לדוגמה, אם הזרימה ב- SB היא 2, תא D5 שווה ל -2.
ב. מהם האילוצים על החלטות אלו? זרימת הנטו (Flow Out - Flow In) של צומת A, B, C, D ו- E צריכה להיות שווה ל 0. במילים אחרות, זרימה החוצה = זרימה פנימה. כמו כן, לכל קשת יש קיבולת קבועה. הזרימה בכל קשת צריכה להיות קטנה מיכולת זו.
ג. מהו המדד הכולל של הביצועים להחלטות אלו? המדד הכולל של הביצועים הוא הזרימה המרבית, ולכן המטרה היא למקסם את הכמות הזו. הזרימה המרבית שווה לזרימה החוצה של צומת S.
2. כדי להקל על ההבנה של המודל, צור את הדברים הבאים טווחים בשם .
| שם טווח | תאים |
|---|---|
| מ | B4: B15 |
| ל | C4: C15 |
| זְרִימָה | D4: D15 |
| קיבולת | F4: F15 |
| דרישת אספקה | K5: K9 |
| מקסימום זרימה | D17 |
3. הכנס את הפונקציות הבאות.

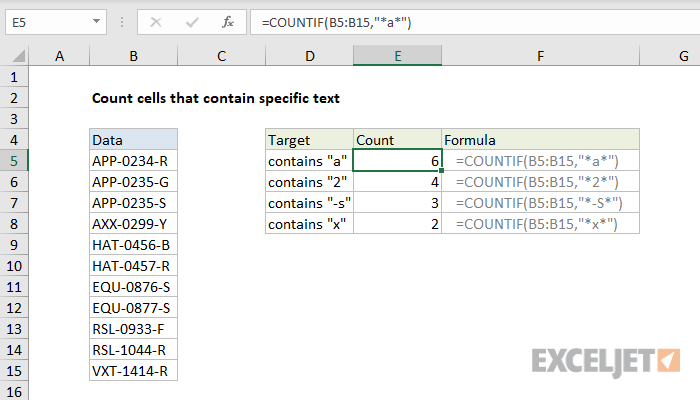
הסבר: ה SUMIF פונקציות מחשבות את זרימת הנטו של כל צומת. עבור צומת A, הפונקציה SUMIF הראשונה מסכמת את הערכים בעמודה זרימה עם 'A' בעמודה מאת (זרימה החוצה). הפונקציה השנייה SUMIF מסכמת את הערכים בעמודה זרימה עם 'A' בעמודה אל (זרימה פנימה). זרימה מקסימלית שווה לערך בתא I4, שהוא הזרימה החוצה מצומת S. מכיוון שלצומת A, B, C, D ו- E יש זרימה נטו של 0, זרימה החוצה מצומת S תהיה שווה לזרימה פנימה של צומת T.
ניסוי וטעייה
בעזרת ניסוח זה, קל לנתח כל פתרון ניסיון.
1. לדוגמה, הנתיב SADT עם זרימה של 2. הנתיב SCT עם זרימה של 4. הנתיב SBET עם זרימה של 2. נתיבים אלה נותנים זרימה כוללת של 8.

כיצד להכין רשימת תבליטים באקסל
אין צורך להשתמש בניסוי וטעייה. בהמשך נתאר כיצד פותר אקסל יכול לשמש כדי למצוא במהירות את הפתרון האופטימלי.
פתור את המודל
כדי למצוא את הפתרון האופטימלי, בצע את השלבים הבאים.
1. בכרטיסיה נתונים, בקבוצה ניתוח, לחץ על פתרון.

הערה: לא מוצאים את כפתור הפותר? לחץ כאן כדי לטעון את תוסף לפתרון .
הזן את פרמטרי הפותר (המשך לקרוא). התוצאה צריכה להיות עקבית עם התמונה שלהלן.

יש לך את האפשרות להקליד את שמות הטווחים או ללחוץ על התאים בגיליון האלקטרוני.
2. הזן את MaximumFlow עבור המטרה.
3. לחץ על מקסימום.
4. הזן זרימה לתאים משתנים משתנים.
5. לחץ על הוסף כדי להיכנס לאילוץ הבא.

6. לחץ על הוסף כדי להיכנס לאילוץ הבא.

7. סמן את האפשרות 'להפוך את המשתנים הבלתי מוגבלים ללא שליליים' ובחר 'Simplex LP'.
8. לבסוף, לחץ על פתור.
תוֹצָאָה:

הפתרון האופטימלי:

מסקנה: הנתיב SADT עם זרימה של 2. השביל SCT עם זרימה של 4. הנתיב SBET עם זרימה של 2. הנתיב SCET עם זרימה של 2. השביל SACET עם זרימה של 1. השביל SACDT עם זרימה של 1. נתיבים אלה נותנים זרימה מרבית של 12.
עבור לפרק הבא: כלי ToolPak לניתוח